▶ 금속 내의 전자운동
▶
에너지대 이론에서 본 도체, 반도체, 절연체
▶
반도체 내의 전자 성질
▶ 반도체의 종류와
성질
▶ 반도체의 전기전도


금속의 내부에서는 무수히 많은 원자가 격자 모양으로 결합되어 있으며, 원자핵에 구속되지 않는 전도 전자가 금속 양이온의 사이를 자유로이 운동하고 있다. 이런 상태의 금속에 전지 등을 사용해 전기장을 가하면 양극을 향해서 전도 전자의 이동이 일어나며, 그 결과 전류가 흐른다는 것을 이미 배웠다.
|
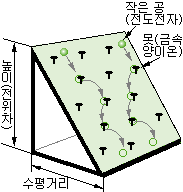
그림 1-29 기울기가 크면 공의 속도가 빨라진다. |
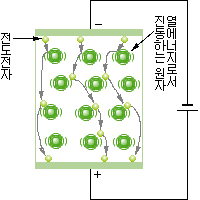
그림 1-30 금속 내의 전자의 이동 |
그림 1-29 는 그 모양을 모형에 의해 나타낸 것인데, 못이 박혀 있는 판을 비스듬히 세워 놓고 위에서부터 작은 공을 굴리면 공이 가속되어 못에 부딪히면서 굴러 내려간다. 전자의 흐름도 공이 굴러 내리는 것과 같이 다수의 전자가 일률적으로 분포한 원자나 금속 양이온 등에 충돌하면서 평균 속도로 이동하고 있다. 또, 그림 1-29 에서 비스듬히 놓아 둔 판의 높이는 전위차에 상당하고, 전위차와 전도 전자의 평균 속도는 서로 비례 관계에 있다. 일반적으로, 상온에 있는 금속도 열에너지를 받아서 금속 양이온이 진동하고 있으므로, 그 사이를 통과하는 전자는 충돌 횟수가 많아지고 열을 발생하게 된다. 또, 이동 속도가 늦어지므로 전류가 감소한다. 이 모양을 나타낸 것이 그림 1-30 이며, 금속의 온도가 상승하는 데에 따라 전기 저항이 증가하는 것도 이런 이유이다. 또, 전도 전자가 한 번 충돌한 다음, 다시 충돌할 때까지의 운동 거리의 평균값을 평균 자유 행정(mean free path)이라 하고, 전자가 이동하는 자유도를 나타내는 것이다. 이 평균 자유 행정은 보통 금속 도체 중에서는 10-4[m] 정도이나, 진공관의 내부 등과 같이 진공에 가까운 곳에서는 운동을 방해 하는 것이 없으므로 10[m] 이상도 되며, 전자만의 자유로운 공간을 만들 수 있다. 다음에는 전자류와 전류의 관계를 알아보기로 한다.
그림 1-30 금속 내의 전자의 이동
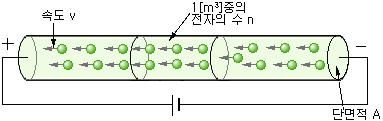
그림 1-31과 같이 도체 중의 전자 밀도를 n[개/m3], 도체의 단면적을 A[m2], 전자의 평균 이동 속도를 v[m/s]로 하면, 1초 동안 이 도체의 단면을 통과하는 전자의 수 N은
![]() -------------------- (1-22)
-------------------- (1-22)
로 된다. 이 식에 전자의 전하 -e[C]를 곱하면, 전류 I는
![]() -------------------- (1-23)
-------------------- (1-23)
가 되며, 전류는 전자의 속도 v에 비례한다. 한편, 평균 속도 v는 전위차, 즉 전압에 비례하므로 옴의 법칙이 성립하는 것도 알 수 있다.