▶ 금속 내의 전자운동
▶
에너지대 이론에서 본 도체, 반도체, 절연체
▶
반도체 내의 전자 성질
▶ 반도체의 종류와
성질
▶ 반도체의 전기전도

금속도체 ◁
반도체 ◁
절연체 ◁
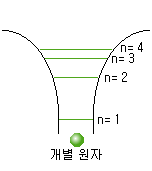
앞에서 배운 바와 같이, 고립 전자가 가지는 에너지는 불연속인 값이 되므로, 그림 1-32와 같은 선으로 나타낼 수 있다.
그림 1-32 고체의 에너지대 구조
그런데 고체에서는 원자가 좁은 간격으로 일정하게 늘어 놓여 있으므로, 원자의 내부만이 아니라 그 상호간에도 영향을 끼치게 된다. 그 결과, 에너지의 값은 다시 작은 단계로 나뉘어져 선 모양이 되고, 전자는 그 중에서 결정된 에너지 값이 궤도에 들어가 있다. 그림 1-32는 원자 간격이 d[m]인 고체의 에너지대 구조를 나타낸 것이다. 바꿔 말하면, 고체 내의 전자가 얻는 에너지 준위는 이와 같이 대(band) 모양으로 되어 있으므로, 고체의 전자 현상을 생각할 때, 에너지대의 구조를 기본으로 한 에너지대 이론(energy band theory)을 쓰면 좋다. 에너지대 구조 중에서 전자가 존재할 수 있는 에너지대를 허용대(allowable band)라 하고, 전자가 존재할 수 없는 에너지대를 금지대(forbidden band) 또는 에너지 갭(energy gap)이라 한다.
|
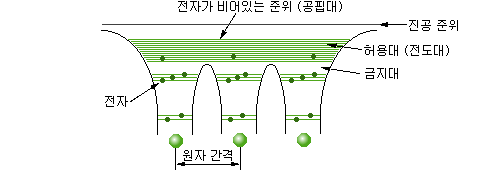
예를 들면, 그림 1-33의 도체의 에너지대 구조에서는, n=3, n=4 의 준위는 전자가 들어갈 수 있는 허용대이고, 전기장을 가하면 전자는 그 반대의 방향으로 이동해서 전류를 흘릴 수 있다. 이와 같이 전자가 자유로이 이동되는 허용대를 전도대(conduction band)라고 한다. 또, 같은 허용대라 하더라도 들어갈 수 있는 전자의 수가 전부 들어가서 전자가 이동할 여지가 없는 허용대를 충만대(filled band)라 하며, 어떤 에너지를 가해 주면 전자가 들어갈 수 있는 허용대라 하더라도 보통의 상태에서는 전자가 존재하지 않는 허용대를 공핍대(exhausion band, empty band)라고 한다.
그림 1-33 도체의 에너지대 구조
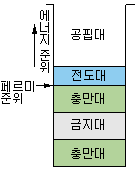
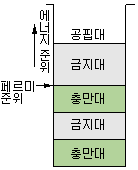
그림 1-34는 도체, 반도체, 절연체의 에너지대 구조를 나타낸 것으로, 이 그림의 가로축 폭은 특별한 의미는 없다.
(a) 금속 도체 |
(b) 반도체 |
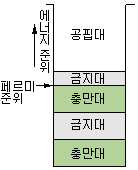
(c) 절연체 |
그림 1-34 충만대와 공핍대
![]()
그림 1-34의 (a)와 같이, 충만대에 공핍대가 접해 있어 공핍대에서는 충만대로부터 전도 전자가 옮겨져서 전도대를 형성하고 있기 때문에 전기 전도가 매우 좋다.
![]()
그림 1-34의 (b)와 같이, 보통 때에는 공핍대에는 전자가 없으며, 또 상위의 충만대와 공핍대와의 사이에 금지대의 폭이 좁다. 그래서 충만대의 일부 전자는 열이나 빛 등의 적은 에너지(1[eV]정도)에서도 비교적 용이하게 금지대를 넘어서 공핍대에 올라갈 수 있다. 이 결과, 너무 올라간 전자는 전도 전자가 되어서 도전성을 가질 수 있게 되나, 그 전도 전자의 수가 적으므로 매우 고저항의 것이 된다. 또, 이때에 그 충만대에는 전자가 빠진 구멍이 생긴다.
![]()
그림 1-34의 (c)와 같이, 전자의 움직임은 반도체와 같다고 보나, 충만대와 공핍대 사이의 에너지 갭이 크므로, 상당히 큰 에너지(6∼7[eV])를 가하지 않으면 충만대의 전자는 공핍대에 올라갈 수 없다. 따라서, 절연체는 도전성을 가질 만큼 큰 전기장을 가하면, 절연 파괴를 일으켜 절연체로서의 역할을 잃고 만다.