▶ 전기장내의 전자운동
▶
자기장내의 전자운동
▶ 전자 빔
▶ 브라운관
▶
연습 문제
원운동의
반지름과 각속도 ◁
나선운동 ◁
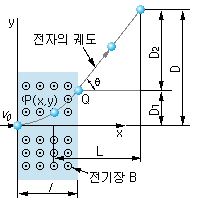
자기장 내에서 정지하고 있는 전자 또는 자기장 방향으로 이동하는 전자는, 그 자기장에 의한 편향력을 받지 않는다. 그러나 그림 1-18과 같이 자기장과 직교하는 방향으로 진입된 전자는, 플레밍의 왼손 법칙에 의한 힘을 받아서 진행 방향이 휘어지게 된다.
그림 1-18 자기장에 직각으로 날아든 전자 |
그림 1-19 전자의 전자 편향 |
그림 1-19는 앞에서 설명한 상태를 평면 위에 나타낸 것으로, 전자는 지면의 뒤에서 앞으로 향하는 자속 밀도 b [Wb/m2]의 평등 자기장 속에서 수직으로 초속도 v0 [m/s]로 진입하는 것으로 한다. 지금, 전자가 나간 거리를 l [m], 전하를 e [C]으로 하면, 전류 I [A]와 l, e, v0과의 사이에는
---------------
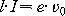(1-15)
의 관계과 성립된다. 따라서, 전자는
-------
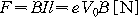(1-16)
의 힘을 받는다. 이 힘 F는 플레밍의 왼손 법칙에 의해 항상 v0의
방향에 직각인 방향이 되므로, 전자는 그림 1-20과 같이 등속 원운동을
한다. 이 때, 자기장에서 전자가 받는 구심력 F [N]과 전자의 원심력
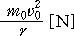은 서로 같으므로,
그림 1.20 자기장 중의 전자의 운동
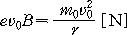-------------------- (1-17)
의 관계가 성립된다. 따라서, 원운동의 반지름 r는 다음과 같이 된다.
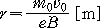-------------------- (1-18)
이와 같이 자기장에 의하여 전자의 진로가 구부러지게 되는 것을 전자 편향 (electromagnetic deflection) 이라고 한다. 또, 원운동의 회전 각속도 ω는 다음과 같이 되고, v0과는 관계가 없다.
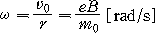-------------------- (1-19)
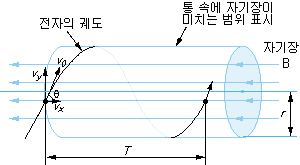
그림 1-21 자기장과 경사지게 진입한 전자의 운동(나선운동)
그림 1-21과 같이 초속도 v0 [m/s]의 전자가 자기장의 방향에 대하여θ 의 각도로 진입하였다고 하자. v0을 자기장 방향의 속도 vx와 수직 방향의 속도 vy로 나누어지며, vx = v0cosθ [m/s], vy = v0sinθ [m/s]가 되고, 오른쪽에서 볼 때에 시계방향으로 원을 그리면서 자기장과 역방향으로 vx = v0cosθ의 속도로 나가는 나선 궤도가 된다. 따라서, 이 때에 나선 운동의 주기 T는 원운동의 주기와 같고, 식 (1-19)에서
-------------------- (1-20)
이 되고, 또 반지름 r는 식 (1-20)에서
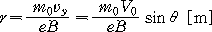--------------- (1-21)
가 된다.
