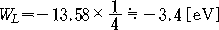▶ 원자와 전자
▶ 원자로부터의 전자기파 방사
▶
전자의 에너지 준위
▶ 연습 문제

에너지장벽 ◁
전자의 에너지 준위 ◁
일함수(Work function)
◁

|
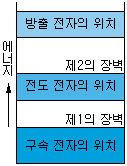
그림 1-5 전자방출에 필요한 에너지 |
금속 도체에 전류가 흐르는 것은 원자핵의 구속에서 빠져 나온 전자, 즉 전도 전자가 금속 안에서 전기장과 역방향으로 가속되어 이동하기 때문이다. 따라서, 금속 내부에서 원자의 표면에는 전자가 원자의 구속으로부터 탈출하는 데에 필요한 에너지에 상당하는 장벽 (barrier layer) 이 있는데, 이 벽을 뛰어넘어 금속 내부를 자유로이 움직일 수 있는 전도 전자라도 그 금속의 표면을 튀어나와 자유 공간으로 이동될 수는 없다. 그것은 다시 큰 제2의 장벽이 있어 이것을 뛰어넘을 만큼의 에너지를 필요로 하기 때문이다. 즉, 전자가 금속 밖으로 나가려 해도 금속 중에 남은 원자의 양전하 사이에 정전력 (eletrostatic force) 이 작용해서 다시 끌어당겨지기 때문이다. 이러한 전자 방출에 필요한 에너지를 띠 (band) 그림으로 나타내면 그림 1-5와 같이 된다.

|
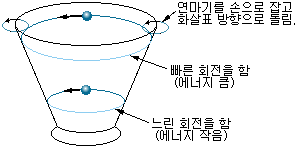
그림 1-6 에너지와 공의 위치 |
그림 1-6과 같이 작은 공을 연마기 모양의 그릇에 넣고 원운동을 시켜 보면, 공을 빨리 돌린 편이 높은 궤도를 돌게 된다. 이와 마찬가지로, 그림 1-7과 같이 전자는 원자핵의 가장자리를 일정한 법칙에 따라 정해진 몇 개의 궤도를 돌고 있다. 이 궤도에는 앞에서 설명한 바와 같이, 안쪽으로부터 붙여진 번호(주 양자수라고 함) 1,2,3,.....,n 에 따라 2n2개의 전자가 안정된 상태로 들어가게 된다. 그리고 주 양자수 n의 궤도를 도는 전자의 에너지 Wn은 수소 원자의 경우
![]() --------------------(1-2)
--------------------(1-2)
로 된다는 것이 알려져 있다. 이 식은, 전자가
가지는 에너지는 원자핵으로부터 멀어지는 정도에 따라 단계적으로 커지고,
그 중간의 에너지를 가지는 전자는 존재하지 않음을 나타내고
있다. 이와 같은 에너지의 불연속의 관계를 에너지
준위(energy level)라 하고, 최저의 준위를 기저 준위라 한다.
식 (1-2)의 '-'부호는 에너지의 기점을 탈출 준위에 놓았기 때문이다.
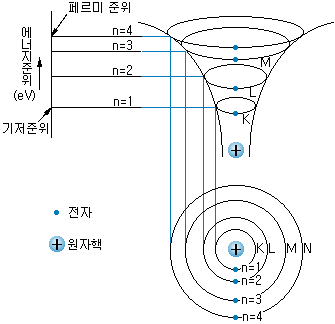
그림 1-7 전자의 에너지 준위

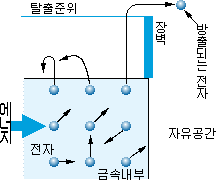
그림 1-8의 (a)에 나타낸 바와 같이, 금속에 열이나 빛 등의 에너지를
가하면 전자는 운동 에너지를 얻어 활발하게 움직이며, 에너지 준위가
높은 몇 개의 전자는 공간으로 방출되고, 이러한 일은 장벽을 뛰어넘을
만큼의 운동 에너지를 얻은 전자만이 자유 공간으로 방출된다고 생각하면
된다. 그림 1-8의 (b)는 이 상태를 에너지 준위로도 나타낸 것이다.
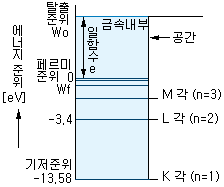
여기서, 장벽의 높이는 전자가 금속면을
탈출하는 데에 필요한 에너지 준위에 상당하는데, 이것을 일함수 (work
function) W라 한다. 또, 장벽의 윗부분은 전자가 금속면을 탈출하는
데에 필요한 에너지 준위에 상당하므로, 탈출
준위 또는 이탈 준위라고 한다. 따라서, 일함수는
탈출 준위(Wo)와 페르미 준위(Wf)와의 차(Wo-Wf) [eV]로 나타낼 수 있다. 페르미
준위 (Fermi level)란, 절대 온도 영도 (0
[。K])에서 가장 밖의 전자(가전자)가 가지는 에너지 높이이다.
일함수는 그 금속의 종류, 표면의 형태 등에 따라 다른 값을 가지고,
흔히 W=eφ로 나타내며, 1개의 전자를 금속체로부터 공간으로 방출하는
데 필요한 일의 양으로 나타낸다. 따라서, 일함수가 작은 물질은 비교적
적은 에너지로 많은 전자를 방출시킬 수 있고, 그 단위는 1[V]의
전위에서 전자에게 주어지는 위치 에너지인 전자볼트 [eV]로
나타낸다.
그러므로 1 [eV] = 1.6×10-19 [J]이다.
그림 1-8 에너지 준위와 장벽
문제 |
L각 전자의 전체 에너지는 얼마가 되겠는가? |
답 |
주 양자수 n개의 궤도를
도는 전자의 에너지 |